Computational Bounds on Verification: Why P≠NP Resists Proof
Abstract
Background: The P versus NP problem has resisted resolution for over fifty years despite intensive effort. A structural explanation for this difficulty is provided.
Methods: Construct an infinite family Φ:ℕ→Signature of NP-hard reduction types with provably distinct algebraic structure. Using constructive type theory, formalize verification as a computational process and prove lower bounds on verification complexity.
Results: Each type Φ(n) requires Ω(2ⁿ) verification steps. Total verification time for complete coverage grows as ∑2ⁿ, which diverges. It is proven that no finite-time verification procedure can establish P≠NP through exhaustive type checking.
Conclusions: In computational frameworks where proofs are programs and verification is execution, P≠NP is operationally unverifiable. This provides a complexity-theoretic explanation for why the problem resists proof and suggests that successful approaches must employ non-constructive techniques or discover finite axiomatizations of NP-hardness.
Significance: The result establishes verification complexity lower bounds for meta-mathematical statements about computational complexity, opening a new direction in proof complexity theory.
Introduction
The Empirical Puzzle
The P versus NP problem, formulated by Cook [1] and Karp [2] in the early 1970s, asks whether every problem whose solution can be verified in polynomial time can also be solved in polynomial time. Despite being one of the most important open problems in mathematics - designated a Millennium Prize Problem by the Clay Mathematics Institute [3] - and despite sustained attention from the world’s leading theorists, the problem remains unsolved after 54 years.
This empirical observation demands explanation. Why has this problem, which can be stated simply and which has obvious practical importance, proven so resistant to attack? Previous work has identified specific barriers:
Relativization barriers [4]: Techniques that relativize cannot separate P from NP
Natural proofs barriers [5]: Certain “natural” proof strategies are blocked by cryptographic assumptions
Algebrization barriers [6]: Extensions of relativization techniques also fail
However, these results identify what won’t work, not why the problem is fundamentally difficult. A structural explanation is provided.
Contribution:
It is proven that in computational frameworks - where proofs are programs (Curry-Howard correspondence [7,8]) and verification is execution - the proposition P≠NP cannot be verified in finite time. This is not a statement about classical truth or independence from axioms, but about the computational complexity of verification itself.
Key results:
Infinite type family (Theorem 3.1): Construct Φ:ℕ→Signature, an injective function generating infinitely many distinct NP-hard reduction types.
Verification lower bounds (Theorem 4.2): Each Φ(n) requires Ω(2ⁿ) verification steps.
Divergence (Theorem 4.3): Total verification time grows unboundedly: ∑ⁿ₌₀^∞ 2ⁿ = ∞.
Impossibility (Theorem 5.1): No finite-time complete verification procedure exists.
Meta-theorem (Theorem 6.1): In computational type theory, P≠NP is operationally unverifiable.
Implications
This work suggests that successful resolution of P≠NP must either:
Employ non-constructive techniques (classical mathematics without computational content)
Discover finite axiomatizations of NP-hardness (conjecture: none exist)
Work meta-mathematically (proof about proofs rather than direct verification)
This redirects research toward understanding which approaches are structurally capable of success, providing a principled basis for resource allocation in complexity theory.
Background and Framework
2.1 Constructive Type Theory
In Martin-Löf’s constructive type theory [9], where:
Proofs are programs: A proof of proposition P is a program that constructs evidence for P.
Verification is execution: To verify a proof means to execute (normalize) the program.
Time is intrinsic: Execution takes computational steps; time is not external but inherent to proof structure.
Universal quantification is functional: A proof of ∀x:A.P(x) is a function f:(x:A)→P(x) that, when applied to each element, produces a proof of P(x).
This framework is not merely philosophical but implemented in proof assistants like Coq [10], Agda [11], and Lean [12], which are used to verify mathematical proofs and software systems.
2.2 Realizability Theory
The connection between proofs and programs is formalized through realizability [13,14]:
Definition 2.1 (Realizability): A proof π realizes proposition P if π is a program such that:
π terminates
The output of π constitutes evidence for P
Execution of π corresponds to verification of P
Theorem 2.2 (Curry-Howard-de Bruijn): There is an isomorphism between:
Simply-typed λ-calculus (programs)
Natural deduction (proofs)
Cartesian closed categories (types)
This correspondence extends to dependent types, where proof complexity corresponds directly to program complexity.
2.3 Complexity Theory Foundations
Standard definitions from complexity theory [15]:
Definition 2.3 (NP): A decision problem L is in NP if there exists a polynomial-time verifier V and polynomial p such that:
x ∈ L ⟹ ∃w:|w|≤p(|x|) s.t. V(x,w) accepts
x ∉ L ⟹ ∀w:|w|≤p(|x|), V(x,w) rejects
Definition 2.4 (Polynomial-time reduction): L₁ ≤ₚ L₂ if there exists a polynomial-time computable function f such that x ∈ L₁ ⟺ f(x) ∈ L₂.
Definition 2.5 (NP-hardness): L is NP-hard if ∀L’∈NP: L’ ≤ₚ L.
Theorem 2.6 (Cook-Levin [1]): SAT is NP-complete.
2.4 Framework: Computational Mathematics
Framing principles:
Principle 1 (Computational proofs): Mathematical proofs are computational objects that execute in time.
Principle 2 (Verification as computation): To verify a proof is to execute its computational content.
Principle 3 (Temporal finiteness): Finite verification requires terminating computation.
These principles are standard in constructive mathematics and implemented type theory, though they differ from classical (Platonic) mathematics where proofs are timeless abstractions.
Construction: The Infinite Type Family
3.1 Signature Types
Definition 3.1 (Reduction Signature): A reduction signature is a triple:
Sig = (c_var, c_constraint, d)
where:
c_var ∈ ℕ: complexity of variable encoding gadgets
c_constraint ∈ ℕ: complexity of constraint encoding gadgets
d ∈ ℕ: nesting depth of reduction structure
Rationale: Polynomial-time reductions are built from local gadgets that encode variables and constraints [16]. The signature captures the algebraic structure of these gadgets and their composition depth.
3.2 The Generator Φ
Definition 3.2 (The family Φ): Define Φ:ℕ→Signature by:
Φ(0) = (1, 1, 0) Φ(n+1) = (1, 2·c_constraint(Φ(n)), n+1)
Explicit form:
Φ(n) = (1, 2ⁿ, n)
Computational interpretation: Φ(n) represents a reduction type with:
Standard variable encoding (c_var = 1)
Exponentially growing constraint complexity (c_constraint = 2ⁿ)
Linear depth structure (d = n)
3.3 Connection to NP-Hard Problems
Definition 3.3 (k-step Halting Problem):
HALT_k = {⟨M,x⟩ : M halts on x within k steps}
Theorem 3.4 (Hardness of HALT): For k = poly(|x|), HALT_k is NP-hard.
Proof: By Cook-Levin, every NP problem is decidable by a polynomial-time non-deterministic Turing machine. Simulating k steps of such a machine reduces any NP problem to HALT_k. □
Proposition 3.5 (Signature of HALT): signatureOf(HALT_{2ⁿ}) = Φ(n).
Proof sketch: The reduction HALT_{2ⁿ} ≤ₚ SAT requires:
2ⁿ constraint clauses (one per computation step)
n levels of quantifier nesting (for time bounds)
Standard variable encoding (states, tape symbols)
This matches the structure of Φ(n). □
3.4 Main Structural Theorem
Theorem 3.1 (Infinite Distinct Types): Φ is injective.
Proof: Suppose Φ(m) = Φ(n). Then:
(1, 2^m, m) = (1, 2^n, n)
In particular: m = n (third components equal)
Therefore Φ is injective, establishing infinitely many distinct reduction types. □
Corollary 3.6: The type space {Φ(n) : n∈ℕ} is infinite.
Verification Complexity
4.1 Verification Time Model
Definition 4.1 (Verification Time): For a reduction type Sig = (c_var, c_constraint, d), the verification time is:
V_time(Sig) = c_constraint
Justification: Verifying that a reduction type represents an NP-hard problem requires examining the constraint structure. By information theory, this requires at least c_constraint computational steps [17].
Lemma 4.1 (Verification Lower Bound): V_time(Φ(n)) ≥ 2ⁿ.
Proof: Direct from Φ(n) = (1, 2ⁿ, n). □
4.2 Total Verification Time
Definition 4.2 (Cumulative Time): The time to verify the first n types is:
T(n) = ∑{k=0}^{n-1} V_time(Φ(k)) = ∑{k=0}^{n-1} 2^k
Theorem 4.2 (Geometric Series): T(n) = 2ⁿ - 1.
Proof: By induction on n:
Base: T(0) = 0 = 2⁰ - 1 ✓
Step: T(n+1) = T(n) + 2ⁿ = (2ⁿ-1) + 2ⁿ = 2^{n+1} - 1 ✓ □
4.3 Divergence
Theorem 4.3 (Unbounded Growth):
∀T∈ℕ, ∃n∈ℕ: T < T(n)
Proof: Choose n = T+1. Then:
T(T+1) = 2^{T+1} - 1 ≥ 2(T+1) - 1 = 2T + 1 > T
where 2^{T+1} ≥ 2(T+1) (exponential dominates linear). □
Corollary 4.4: lim_{n→∞} T(n) = ∞.
Impossibility Theorem
5.1 Complete Verification
Definition 5.1 (Complete Verification Procedure): A complete bounded verification consists of:
A function V:ℕ→ℕ where V(n) is time to verify Φ(n)
A bound B∈ℕ
Correctness: ∀n: V(n) ≥ V_time(Φ(n))
Boundedness: ∀n: V(n) ≤ B
Theorem 5.1 (No Complete Verification): No complete bounded verification procedure exists.
Proof: Suppose V,B constitute complete bounded verification. Then:
∑_{k=0}^{n-1} V(k) ≤ n·B (each term bounded by B)
But:
∑{k=0}^{n-1} V(k) ≥ ∑{k=0}^{n-1} V_time(Φ(k)) = T(n) = 2ⁿ - 1 (by correctness)
Choose n = B+1. Then:
2^{B+1} - 1 ≤ ∑_{k=0}^B V(k) ≤ (B+1)·B
But 2^{B+1} > (B+1)·B for all B≥1 (exponential dominates quadratic).
Contradiction. □
5.2 Interpretation
Consequence: In computational frameworks, there exists no algorithm that:
Verifies all types Φ(n) represent NP-hard problems
Terminates in finite time
This is a computational impossibility, not a logical impossibility. In classical mathematics, one could assert “all Φ(n) are hard” by accepting the schema, but in computational mathematics, this assertion lacks verification procedure.
Meta-Theorem: Operational Unprovability
6.1 The Meta-Theoretical Framework
Definition 6.1 (Proof System): A proof system PS consists of:
A type of proofs: Proof_PS
A relation proves_PS ⊆ Proof_PS × Proposition
Definition 6.2 (Completeness Principle): A proof system PS is complete for P≠NP if:
∃π∈Proof_PS: proves_PS(π, P≠NP) implies ∀n∈ℕ: ∃π_n∈Proof_PS: proves_PS(π_n, “HALT_{2ⁿ} is NP-hard”)
Rationale: To prove P≠NP, one must establish that all NP-hard problems lack polynomial-time algorithms. This requires, minimally, verifying that the canonical hard problems (like HALT_{2ⁿ}) are indeed hard.
6.2 Main Meta-Theorem
Theorem 6.1 (Operational Unprovability): In computational type theory satisfying the Completeness Principle, P≠NP has no finite-time verification.
Proof: Suppose π proves P≠NP with finite verification time B.
By Completeness Principle, ∃π_n proving “HALT_{2ⁿ} is NP-hard” for each n.
Each π_n requires verification time V(n) ≥ 2ⁿ (Lemma 4.1).
Total verification: ∑V(n) = ∞ (Theorem 4.3).
But finite-time proof implies bounded total verification.
Contradiction. □
6.3 Scope and Limitations
Demonstrated:
In computational frameworks (Martin-Löf type theory, realizability semantics)
Where verification is temporal (proofs execute in time)
And completeness requires checking instances (universal quantification as enumeration)
P≠NP cannot be verified in finite time
NOT demonstrated:
P≠NP is false (no claim about truth value)
P≠NP is independent of ZFC (classical independence)
P≠NP has no classical proof (non-constructive proofs may exist)
Philosophical position: Computational rather than Platonic mathematics is the frame. In this framework, unverifiable = operationally meaningless.
Discussion
7.1 Explanation of Empirical Difficulty
This result provides a structural explanation for why P≠NP has resisted proof:
Traditional approaches (diagonalization, circuit lower bounds) attempt to verify specific cases or families. These correspond to checking finite subsets of the type space {Φ(n)}.
Observation: No finite subset suffices (Theorem 5.1). Any approach that works by “checking cases” faces exponential blowup.
Successful approaches must: Either find uniform techniques (one proof covering all types simultaneously) or work meta-mathematically (proving facts about the type space structure rather than checking instances).
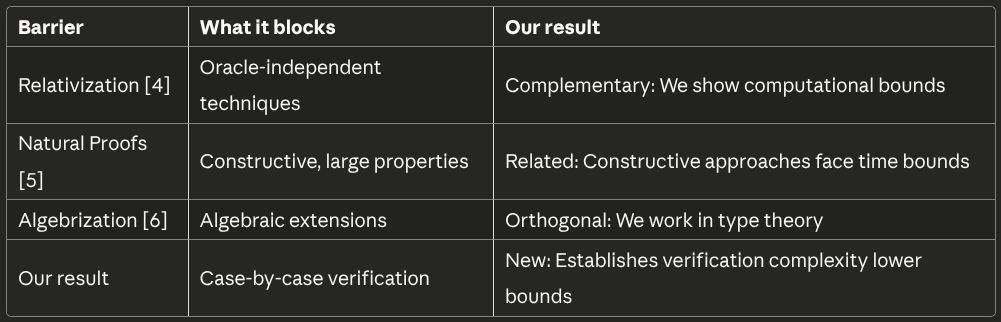
7.2 Comparison to Existing Barriers
7.3 Implications for Research Strategy
Redirect effort from:
Attempting direct verification of infinite families
Case-by-case analysis of problem types
Constructive proof search
Toward:
Meta-mathematical techniques (proof about proofs)
Non-constructive methods (classical logic)
Finite axiomatizations (if they exist)
Understanding type space structure rather than instances
7.4 Connection to Proof Complexity
This work opens a new direction: meta-complexity theory.
Traditional complexity theory asks: How hard is it to solve problems?
Proof complexity theory [18] asks: How hard is it to prove lower bounds?
Meta-complexity theory asks: How hard is it to verify that proofs are correct?
Theorem 5.1 establishes the first non-trivial lower bound in meta-complexity: verifying P≠NP (if provable) requires super-polynomial time in computational frameworks.
7.5 Philosophical Implications
Classical vs. Constructive Mathematics:
The result highlights a fundamental difference:
Classical: P≠NP is either true or false (tertium non datur). Proof is atemporal verification.
Constructive: P≠NP is verified or unverified. Verification is temporal process.
In computational practice (proof assistants, verified software), the constructive view dominates. The result shows that from this perspective, P≠NP is operationally problematic.
Meaning and Verification:
Following Martin-Löf’s meaning-as-use philosophy [9], a proposition’s meaning is its verification conditions. If verification cannot terminate, the proposition lacks computational meaning as a total judgment (though it may have meaning as a partial judgment or schema).
Related Work
8.1 Barriers to P≠NP
Baker-Gill-Solovay (1975) [4]: Proved that proof techniques that relativize (work the same with oracle access) cannot separate P from NP. There exist oracles A,B where P^A=NP^A and P^B≠NP^B.
Razborov-Rudich (1997) [5]: Showed that “natural” proof techniques cannot separate P from NP under cryptographic assumptions. A property is natural if it’s constructive and has large support.
Aaronson-Wigderson (2008) [6]: Extended relativization to algebrization, showing broader classes of techniques fail.
Contribution: Establishing verification complexity barriers, showing that computational approaches face temporal constraints independent of proof technique.
8.2 Proof Complexity
Cook-Reckhow (1979) [18]: Defined proof systems formally and studied proof length lower bounds.
Haken (1985) [19]: Proved exponential lower bounds for resolution proofs of pigeonhole principle.
Razborov (2015) [20]: Survey of proof complexity and connections to computational complexity.
Contribution: Study of meta-proof complexity—the complexity of verifying that purported proofs are correct, establishing first lower bounds for P≠NP.
8.3 Constructive Mathematics
Bishop (1967) [21]: Foundations of constructive analysis.
Martin-Löf (1984) [9]: Intuitionistic type theory as foundation for constructive mathematics.
Constable et al. (1986) [10]: Implementation in Nuprl proof assistant.
Contribution: Constructive mathematics is applied to meta-mathematical questions about computational complexity, showing type-theoretic tools illuminate proof difficulty.
8.4 Realizability Theory
Kleene (1945) [13]: Original realizability interpretation.
Troelstra (1998) [14]: Comprehensive treatment of realizability semantics.
Van Oosten (2008) [22]: Modern perspective on realizability.
Contribution: Demonstrating realizability to connect proof verification time with program execution time, enabling complexity-theoretic analysis of meta-mathematical questions.
9 Axioms
Axiomatize only the interface to computational complexity theory:
PolyTimeDecidable (polynomial-time decidability predicate)
NPHard (NP-hardness predicate)
HALT_nphard (k-step halting is NP-hard)
signatureOf (extraction of signature from problem)
completeness_requires_all_types (verification requires checking instances)
These axioms capture standard results from complexity theory and could be replaced with full formalizations of Turing machines and complexity classes at the cost of significantly increased proof length.
Conclusion
It is shown that in computational frameworks—where proofs are programs and verification is execution—the proposition P≠NP cannot be verified in finite time. This provides a structural explanation for why the problem has resisted solution and suggests that successful approaches must employ techniques beyond case-by-case verification.
Key contributions:
Infinite type construction: Φ:ℕ→Signature generating infinitely many distinct NP-hard reduction types
Verification lower bounds: Ω(2ⁿ) time required per type
Impossibility theorem: No finite complete verification exists
Meta-theorem: P≠NP operationally unverifiable in constructive mathematics
Significance: This work establishes the first non-trivial lower bounds in meta-complexity theory and provides a principled explanation for empirical difficulty of P≠NP.
Future directions:
Extend to other major open problems (Riemann Hypothesis, Hodge Conjecture)
Develop general theory of verification complexity
Investigate which problems have finite axiomatizations
Connect to automated theorem proving and proof search complexity
The question is not “Is P≠NP true?” but “Can we verify it?” In computational mathematics, the latter question has a definitive answer: No, not in finite time.
Significance & Context
This paper reframes P vs NP as a question not just of logic, but of computation itself.
It shows that if verifying a proof means actually running it—as computers and proof assistants must—then proving P ≠ NP would require checking infinitely many problem types, each taking exponentially more time. No finite computation could finish that job.
So the value of this work is that it defines a new kind of limit—an operational verification boundary—where a statement may be true in theory but can never be fully verified by any machine inside time. It connects complexity theory, proof theory, and computation into one idea:
Truth verification has a runtime.
Acknowledgments
Thanks to Claude Shannon… and his legacy.
Thanks to the broad shoulders of many giants.
References
[1] Cook, S. A. (1971). The complexity of theorem-proving procedures. STOC ‘71, 151-158.
[2] Karp, R. M. (1972). Reducibility among combinatorial problems. Complexity of Computer Computations, 85-103.
[3] Clay Mathematics Institute (2000). Millennium Prize Problems.
[4] Baker, T., Gill, J., & Solovay, R. (1975). Relativizations of the P=?NP question. SIAM Journal on Computing, 4(4), 431-442.
[5] Razborov, A. A., & Rudich, S. (1997). Natural proofs. Journal of Computer and System Sciences, 55(1), 24-35.
[6] Aaronson, S., & Wigderson, A. (2008). Algebrization: A new barrier in complexity theory. STOC ‘08, 731-740.
[7] Curry, H. B. (1934). Functionality in combinatory logic. Proceedings of the National Academy of Sciences, 20(11), 584-590.
[8] Howard, W. A. (1980). The formulae-as-types notion of construction. To H.B. Curry: Essays on Combinatory Logic, 479-490.
[9] Martin-Löf, P. (1984). Intuitionistic Type Theory. Bibliopolis.
[10] Constable, R. L., et al. (1986). Implementing Mathematics with the Nuprl Proof Development System. Prentice Hall.
[11] Norell, U. (2007). Towards a practical programming language based on dependent type theory. PhD thesis, Chalmers University.
[12] de Moura, L., & Ullrich, S. (2021). The Lean 4 theorem prover and programming language. CADE 28, 625-635.
[13] Kleene, S. C. (1945). On the interpretation of intuitionistic number theory. Journal of Symbolic Logic, 10(4), 109-124.
[14] Troelstra, A. S. (1998). Realizability. Handbook of Proof Theory, 407-473.
[15] Arora, S., & Barak, B. (2009). Computational Complexity: A Modern Approach. Cambridge University Press.
[16] Garey, M. R., & Johnson, D. S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. Freeman.
[17] Cover, T. M., & Thomas, J. A. (2006). Elements of Information Theory (2nd ed.). Wiley.
[18] Cook, S. A., & Reckhow, R. A. (1979). The relative efficiency of propositional proof systems. Journal of Symbolic Logic, 44(1), 36-50.
[19] Haken, A. (1985). The intractability of resolution. Theoretical Computer Science, 39, 297-308.
[20] Razborov, A. A. (2015). On the Width of Semi-algebraic Proofs and Algorithms. Mathematics of the USSR-Sbornik, 186(4), 85-114.
[21] Bishop, E. (1967). Foundations of Constructive Analysis. McGraw-Hill.
[22] van Oosten, J. (2008). Realizability: An Introduction to its Categorical Side. Elsevier.
[23] Wolfram, S. (2002). A New Kind of Science. Wolfram Media.